include "math.m";
math:= load Math Math->PATH;

dot         : fn(x, y: array of real)  : real;
norm1, norm2: fn(x: array of real)     : real;
iamax       : fn(x: array of real)     : int;
gemm        : fn(transa, transb: int, # upper case N or T
                 m, n, k: int, alpha      : real,
                 a: array of real, lda    : int,
                 b: array of real, ldb    : int, beta: real,
                 c: array of real, ldc    : int);
sort        : fn(x: array of real, p: array of int);

   dot(x, y) = sum(x [i]* y [i])   
        norm1(x) = sum(fabs(x [i]))   
        norm2(x) = sqrt(dot(x, x))

The convention is assumed that matrices are represented as singly-subscripted arrays with Fortran storage order. So for an m by n matrix A, loops are used with 0<= i < m and 0<= j < n and access is A [i + m *j].

Rather than provide the huge number of entry points in BLAS2 and BLAS3, Inferno provides the matrix multiply primitive, gemm, defined by

A = a* A'*B' + 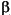*C where the apostrophes indicate an optional transposition. As shown by the work of Kagstrom, Ling, and Van Loan, the other BLAS functionality can be built efficiently on top of gemm.

Matrix a ' is m by k, matrix b ' is k by n, and matrix c is m by n. Here a ' means a (a ') if transa is the constant N (T), and similarly for b '. The sizes m, n, and k denote the active part of the matrix. The parameters lda, ldb, and ldc denote the leading dimension or size for purposes of indexing. So to loop over c use loops with 0<= i < m and 0<= j < j and access a [i +ldc *j].

The sorting function sort (x, p) updates a 0-origin permutation p so that x [p[i]] <= x [p[i+1]], leaving x unchanged.

See Also

Bo Kagstrom, Per Ling, and Charles Van Loan. Portable high performance GEMM-based level 3 BLAS. In R.F. Sincovec et al., editor, Parallel Processing for Scientific Computing, pages 339-346. SIAM Publications, 1993.